
If a fundamental drainage problem is suspected, thicker layers may only be of marginal benefit – a better solution is to address the actual drainage problem by using very dense layers (to minimize water infiltration) or designing a drainage system. Keep in mind that a drainage coefficient is basically a way of making a specific layer thicker. Generally, quick-draining layers that almost never become saturated can have coefficients as high as 1.4 while slow-draining layers that are often saturated can have drainage coefficients as low as 0.40. Additionally, all layers below the HMA layer are assigned a drainage coefficient (m) that represents the relative loss of strength in a layer due to its drainage characteristics and the total time it is exposed to near-saturation moisture conditions. The Structural Number is converted to actual layer thicknesses (e.g., 150 mm (6 inches) of HMA) using a layer coefficient (a) that represents the relative strength of the construction materials in that layer.

The Structural Number is an abstract number expressing the structural strength of a pavement required for given combinations of soil support (M R), total traffic expressed in ESALs, terminal serviceability and environment. The pavement structure is characterized by the Structural Number (SN).
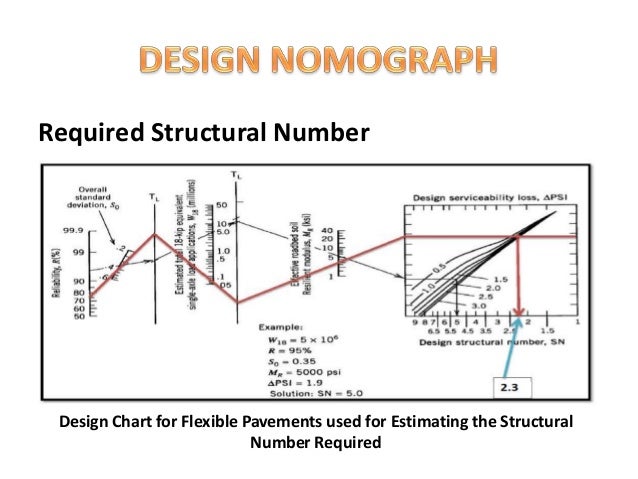
The Z R and S o variables account for reliability. In other words, there must be some assurance that a pavement will perform as intended given variability in such things as construction, environment and materials. The reliability of the pavement design-performance process is the probability that a pavement section designed using the process will perform satisfactorily over the traffic and environmental conditions for the design period (AASHTO, 1993 ). The predicted loading is simply the predicted number of 80 kN (18,000 lb.) ESALs that the pavement will experience over its design lifetime. The 1993 AASHTO Guide equation requires a number of inputs related to loads, pavement structure and subgrade support. This can lead to invalid results at the least and incorrect results at the worst. Otherwise, it is quite easy to use an equation with conditions and materials for which it was never intended. When using the 1993 AASHTO Guide empirical equation or any other empirical equation, it is extremely important to know the equation’s limitations and basic assumptions.

The rest of this section will discuss the specific assumptions, inputs and outputs associated with the 1993 AASHTO Guide flexible pavement empirical design equation.

This equation is not the only empirical equation available but it does give a good sense of what an empirical equation looks like, what factors it considers and how empirical observations are incorporated into an empirical equation. Structural Number (an index that is indicative of the total pavement thickness required)Ī 1D 1 + a 2D 2m 2 + a 3D 3m 3+…a i = ithlayer coefficientD i = i thlayer thickness (inches)m i = i th layer drainage coefficientĭifference between the initial design serviceability index, po, and the design terminal serviceability index, pt Predicted number of 80 kN (18,000 lb.) ESALsĬombined standard error of the traffic prediction and performance prediction


 0 kommentar(er)
0 kommentar(er)
